문제 번호 : 16938
문제 출처 : https://www.acmicpc.net/problem/16938
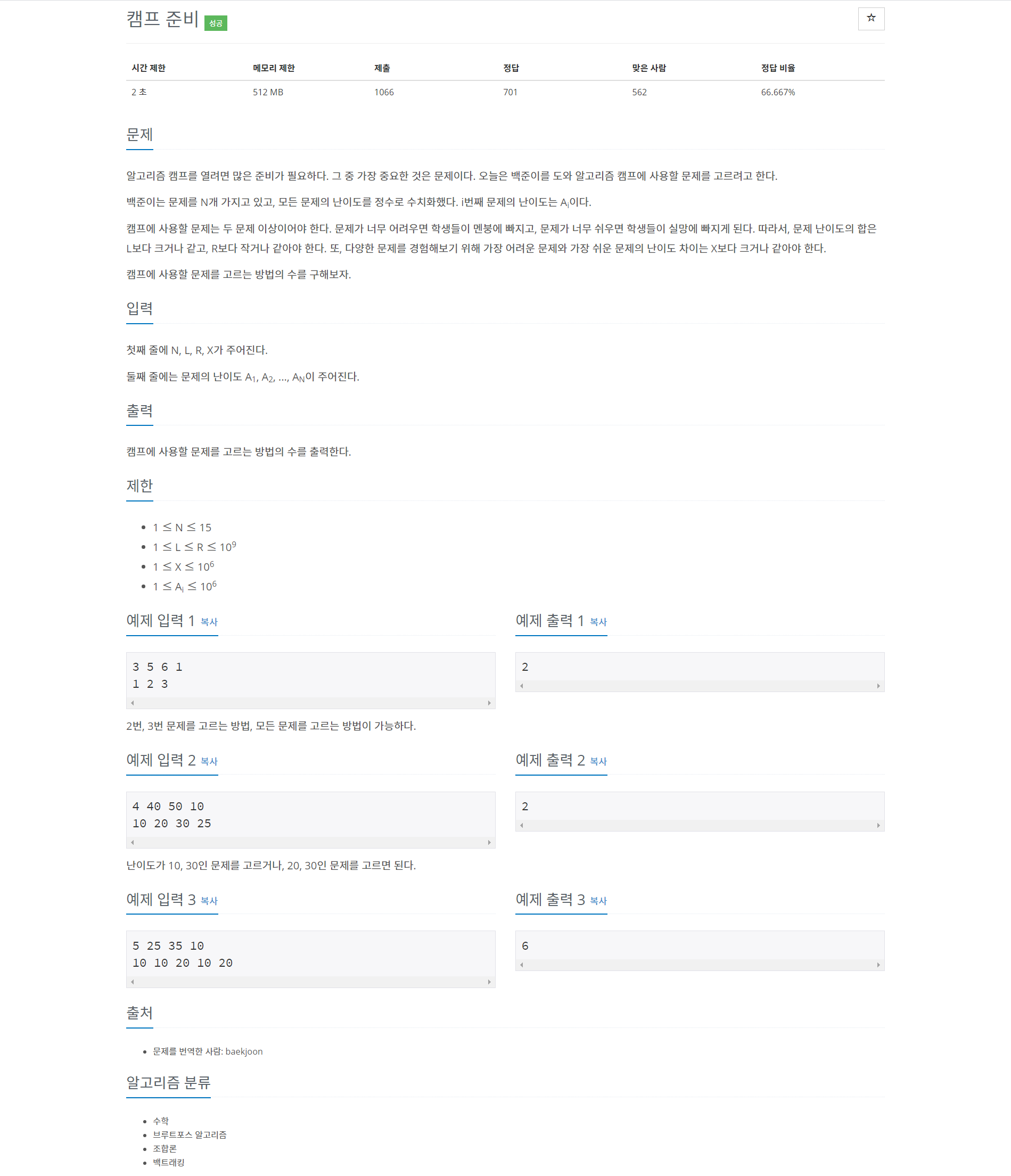
16938번: 캠프 준비
난이도가 10, 30인 문제를 고르거나, 20, 30인 문제를 고르면 된다.
www.acmicpc.net
Code
import itertools
def diff(num):
return max(num) - min(num)
n, l, r, x = map(int, input().split())
a = list(map(int, input().split()))
count = 0
for i in range(2, n+1):
numbers = list(itertools.combinations(a, i))
for number in numbers:
if l <= sum(number) <= r:
if diff(number) >= x:
count += 1
print(count)Idea
- N개의 난이도를 2개 이상으로 조합해서 조건에 맞는지 확인한다.
- combination한 후 list의 요소는 iterable한 튜플 형으로 모든 난이도의 합은 sum 함수로 구현이 가능하다.
- 차를 구하는 함수는 최대값에서 최소값을 빼주는 형태로 가능했다.
- 두 조건을 모두 만족하면 count 값을 1씩 증가시키고 마지막에 출력한다.
이전의 문제들보다 난이도가 낮은 편이었다. 처음에는 n이 1인 경우에 print(0)을 먼저 하는 경우를 생각했었는데 print를 2번하게 되어서 채점중(99%)에서 "틀렸습니다"가 나왔다. 아무래도 마지막 입력에서 n이 1인 듯하다. n이 1이면 2개 이상을 조합으로 뽑아올 수 없다.
'프로그래밍 > BAEKJOON' 카테고리의 다른 글
| [백준][파이썬] 16637번 괄호 추가하기 (0) | 2021.07.19 |
|---|---|
| [백준][파이썬] 16943번 숫자 재배치 (0) | 2021.07.19 |
| [백준][파이썬] 16937번 두 스티커 (0) | 2021.07.18 |
| [백준][파이썬] 16936번 - 나3곱2 (0) | 2021.07.17 |
| [백준][파이썬] 16924번 - 십자가 찾기 (0) | 2021.07.17 |